Phase Field

Building of Bridges using Phase Field Method

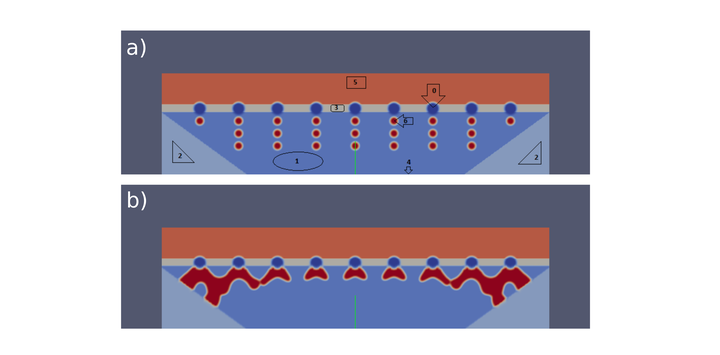
In civil engineering, shape optimization is necessary to build strong structures according to their structural performances. Most structural optimizations take into account structural performances such as stress, mass, deformation. In this work, we have partially optimized the shape of a bridge which connects two banks of a river. To build the strong bridge to withstand high mechanical loads, we have used the technique of growing high strength material in the place of high stress areas, and filled the remaining place with a soft and low weight material such as ‘air’. The ‘growth’ of the high strength material in high stress fields has done based on the Phase Field method. The key idea used is the replacement of actual shape optimization problem by a two phase material distribution problem. The two materials used are the high contrast in their strength properties, a matrix material and a high strength material in the form of inclusions. Phase field method was used to find the motion of optimized shape boundaries. To solve the multicomponent phase field equations, an open source library called ‘OpenPhase’ developed at Prof. Ingo Steinbach department, ICAMS, has been used.

The above figure shows: (a) Initialization of different areas of a bridge with different phases, (b) A partially optimized arc shape of the bridge (every pole has the same eigenstrain)

A C++ code has been written to initialize the model with different phases representing different material properties in the OpenPhase source code. The driving force is assigned to the inclusion material in such a way that it grows in the region where the stresses are high. From the results, we observed that the shape of the optimized structure looks like a semicircle arc shape. Here, we have not taken the idle values of the input parameters for the surrounding environments like water and air etc., so the arc shape is not fully formed. Some more work has to be done to complete the arc shape bridge. However, based on the primary results, we have showcased that the structures can be optimized with Phase Fields using the OpenPhase code.